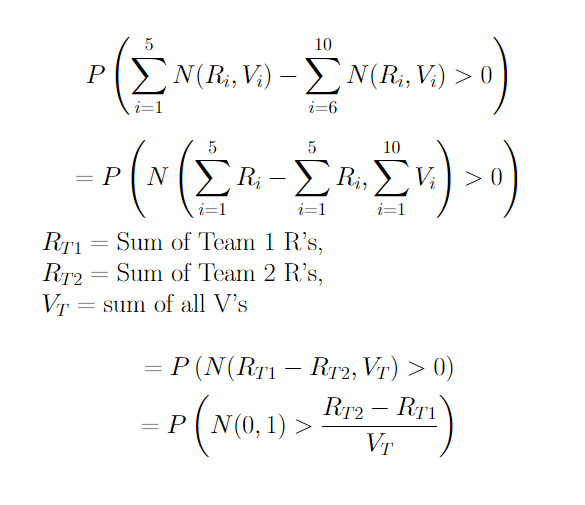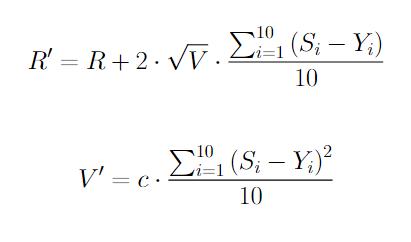Designing a Rating System for Esports
Defining Criteria
Elo, Glicko, TrueSkill all serve their purpose but have shown to have their flaws that can annoy players. So today, let’s try to design a rating system that is designed for team-based esports from the ground up. First, we have to define what our rating system needs to do:
Be predictive of winning odds
Adjust based on win/loss and severity
Also adjust based on relative player performance
Quickly adapt to large loss/win streaks
These criteria are somewhat subjective, but after being in the ranked/competitive sphere of multiple games, these are generally things that I have found that players want.
Core Variables
The first thing to note is that we want our model to be predictive so to an extent we need to guess the relative odds of a player winning. To do this, we can define two numbers for each player. R will be their mean rating and V will be their volatility. You can think of these as the mean and variance of how the player performs. A player with higher performance rating will be expected to play better and a player with higher volatility will be expected to have larger swings in performance.
Predictor Usage
Now here comes some math. If players 1-5 are on team 1 with performance ratings of R1, R2, … , R5 and volatilities V1, V2, … , V5 and players 6-10 are on team 2 with similarly labeled ratings and volatilities, then we can say that the expected outcome is predicted by the probability that the difference of the sum of the distributions of ratings of each team is greater than 0. Alternatively: P(Sum(N(Ri, Vi), i = 1 to 5) - Sum(N(Ri, Vi), i = 6 to 10) > 0) is the probability that team 1 wins. Doing a bit more math:
From here, we can just use a lookup table to find the appropriate probability. As you can see, it depends on the relative combined skills of each team and how volatile the players are, which makes sense in practice. The team that is higher skilled on average is more likely to win, but the more volatile players are, the closer the odds are to being a coin flip.
Updating Values
Now, we have to figure out how to update player’s rating and volatility to maintain this property. The simplest way to do this is take the last several games (lets use 10 as an example) and calculate the expected performance of the player then compare it to the actual performance. Instead of calculating based on the rating of the player during that game, though, we would calculate all 10 games based on the player’s current rating and volatility. This makes updates more responsive to win/loss streaks and calculates relative performance to the current rating, which should make it converge to the player’s true skill faster.
Game Outcomes and Player Performance
We would like to convert each win/loss/draw in the player’s match history to a value between 0 and 1. In games with only binary/ternary outcomes, this would just translate as win = 1, loss = 0, draw = 0.5, but in games with more granular outcomes (such as round differential), we want to translate the outcome to a real value between 0 and 1. For example, if a team wins 13-7 rounds, the outcome would be 0.65, but a 13-2 would be 0.87. For the first game we can call this S1, for the second game S2 and so on.
If it is possible to account for player performance, we would like to adjust these outcomes to reflect how much the player contributed. I will not describe a specific per-game player performance scoring system (as that is very much dependent on the game), but lets assume we have one. First thing we need to do is scale it to the range -1 to 1, where -1 indicates that the player played as poorly as possible, 1 indicates that the player was benefitting their own team to the maximum possible extent, and 0 would indicate the player played an average game. Now since we know a draw is 0.5, we can scale relative to that. For a win, we can scale it such that we linearly interpolate between 0.5, the actual score of the game, and 1 using -1, 0, 1 as our input breakpoints. For a loss, we would do a similar thing, but with 0, the actual score of the game, and 0.5 being the values to interpolate between. A few examples:
A player scored at 1 on a win would receive a 1 no matter the actual game score
A player scored at -1 on a loss would receive a 0 no matter the actual game score
A player scored at 0 on a win or a loss would receive the actual game score
If this individual performance scoring system is available, we adjust S1, S2, … , S10 accordingly, otherwise we use the S values as is.
Expected Outcomes
Once we do this for the last 10 games of a player, we need to calculate the predicted outcome for each game. To do this, we would need to save the player’s team’s rating sum (not including the player) (call it RT1), the enemy team’s rating sum (call it RT2), and the volatility sum of all players (not including the player we are calculating for) (call it VT). Now for that game we calculate Y = P(N(0, 1) > (RT1 + R - RT2)/(VT + V)), where R and V are the player’s current rating. We do this for all 10 games, calling the outcomes Y1, Y2, … ,Y10.
Adjustment Calculations
Once we have all the needed values, we are ready to adjust the player’s R and V.
This sets R’ as R shifted two standard deviation times the mean outcome delta and V’ as the variance of outcome times a constant, c (which just has to be greater than 0). This helps account for win/loss streaks as a high discrepancy in performance vs expectation will result in larger shifts.
Displaying Rating for the Player
From a given R and V, if you’d like to display to the player a certain rating, there are a few options:
Conservative: Rating = R - 2*sqrt(V). This rating is about 95% (assuming normal distribution) certain of true rating.
Mean: Rating = R. This rating is an estimate of the true rating.
Mean and Volatility: Rating = R, V. This shows the player both an estimate of their rating and how volatile it is.
Rating value can be scaled and shifted by constant values to adjust into desirable ranges (and probably should be as R has a mean value of 0). Volatility (if displayed) can be scaled by a positive value but should realistically not be shifted if the meaning of the value is to be preserved.
As a nice, short name we can call this rating system the PRAV (Predictive Rating and Volatility) system.